Python 大O符號
Python 大O符號
必須分析算法的效率和準確性,以便對它們進行比較,并為特定場景選擇特定的算法。進行這種分析的過程稱為漸近分析。它是指以數學計算單位計算任何操作的運行時間。例如,一個操作的運行時間被計算為f(n),并且可能針對另一個操作被計算為g(n2)。這意味著第一次運行時間將隨著n的增加而線性增加,第二次運行的運行時間將隨著n的增加呈指數增長。同樣,如果n很小,兩個操作的運行時間將幾乎相同。
通常,算法所需的時間分為三種類型 -
- 最佳案例 - 程序執行所需的最短時間。
- 平均情況 - 程序執行所需的平均時間。
- 最差情況 - 程序執行所需的最長時間。
漸近符號
以下是計算算法運行時間復雜度的常用漸近符號。
- Ο表示法
- Ω符號
- θ符號
大O符號
符號Ο(n)是表達算法運行時間上限的形式化方式。它測量算法可能需要完成的最壞情況時間復雜度或最長時間。
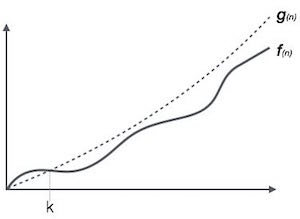
例如,對于函數 f (n)
Ο( _f_ (n)) = { _g_ (n) : there exists c > 0 and n0 such that _f_ (n) ≤ c. _g_ (n) for all n > n0. } 歐米茄符號Ω
符號Ω(n)是表達算法運行時間下限的形式化方式。它可以衡量算法可能需要完成的最佳案例時間復雜度或最佳時間量。
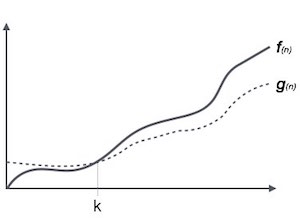
例如,對于函數 f (n)
Ω( _f_ (n)) ≥ { _g_ (n) : there exists c > 0 and n0 such that _g_ (n) ≤ c. _f_ (n) for all n > n0. } Theta符號θ
符號θ(n)是表達算法運行時間的下限和上限的形式化方式。它表示如下 -
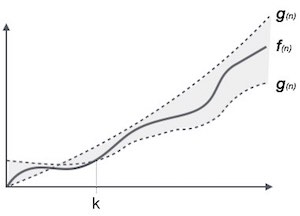
θ( _f_ (n)) = { _g_ (n) if and only if _g_ (n) = Ο( _f_ (n)) and _g_ (n) = Ω( _f_ (n)) for all n > n0. }
常用的漸近符號
以下是一些常見漸近符號的列表 -
| 不變 | \- | Ο(1) |
| 對數的 | \- | Ο(log n) |
| 線性 | \- | Ο(n)的 |
| nlogn | \- | Ο(n log n) |
| 二次 | \- | Ο(n 2) |
| 立方體 | \- | Ο(n 3) |
| 多項式 | \- | ? Ο(1) |
| 指數 | \- | 2 (n) |
相關文章
- Python 中文編碼
- Python for 循環語句
- Python 正則表達式
- Python 排序算法
- Python3 基礎語法
- Python3 集合(Set)
- Python3 多線程
- Python File close() 方法
- Python os.fpathconf() 方法
- Python os.minor() 方法
- Python os.readlink() 方法
- Python os.remove() 方法
- Python os.renames() 方法
- Python os.tmpnam() 方法
- Python center()方法
- Python isalpha()方法
- Python rindex()方法
- Python List reverse()方法
- Python 字典 Dictionary cmp()方法
- Python 字典 Dictionary copy()方法




